| Modern electronics is developing at a staggering pace, with digital electronics leading the exponential expansion in all areas of our life. So it should be reasonable to expect that an 80 year old concept of analog electronic signal amplification, after being through various technological phases, from vacuum thermionic tubes to highly advanced compound semiconductor devices, would these days be considered well known and understood, old fashioned, trivial, almost obsolete. Well, not quite. |
 Wideband Amplifiers by Peter Starič and Erik Margan 3rd reprint, in color, also available as e-book (in PDF) (Springer, http://www.springer.com/gp/book/9780387283401) First I must express my gratitude to my friend Nenad Bach for allowing and enabling this presentation of Peter's and my work on CROWN pages. - Erik Margan It occurs rarely that a book, which has been published some 10 years ago, and at the time received excellent review marks, but not high selling numbers (mostly owed to its highly specialized subject area and a relatively demanding mathematical treatment) is honored by the publisher with a third printout, this time in full color, and also appearing as an e-book online. Modern electronics is developing at a staggering pace, with digital electronics leading the exponential expansion in all areas of our life. So it should be reasonable to expect that an 80 year old concept of analog electronic signal amplification, after being through various technological phases, from vacuum thermionic tubes to highly advanced compound semiconductor devices, would these days be considered well known and understood, oldfashioned, trivial, almost obsolete. Well, not quite so. The thing is that digital electronics, advanced as it may be, must still eventually be interfaced to the real world, most conveniently in analog form, both at the signal input and output stages. From simple microphones converting sound or other mechanical vibration energy to electric signals, temperature sensors, photodiodes for light detection, to such extreme cases as high energy particle detectors at the heart of the ATLAS experiment at the CERN's Large Hadron Collider, analog electronics is still pretty much ubiquitous and indispensable. Actually, analog electronics, and simple amplifier circuits in particular, are met by most electronics engineers very early in their university curricula, forming the base examples of electronics application and serving as simple models for learning the art of circuit analysis and design. However, whilst the analytical mathematical procedures for describing the circuit behavior in the frequency domain has transitionally received a thorough treatment and full depth presentation in engineering curricula, the complementary, but equally important analysis in the time domain is generally limited to most elementary examples, and is abandoned as soon as the system complexity increases beyond the ability to represent it by a first-order linear differential equation. It was therefore felt by us the authors of the book that the importance of proper treatment of electronics systems in the time domain represents a necessary prerequisite for the understanding and development of better systems, especially in regard of ever higher speed and precision requirements in signal processing, coupled to a contemporary reduction of power consumed. Most of the material in the book relates to the problems encountered in the analysis and design of oscilloscope vertical amplifiers, and a considerable part of it has been long held a trade secret. Oscilloscopes are those laboratory instruments which allow you to view the shape of an electric signal in real time, thus helping enormously both the serviceman and the design engineer to quickly identify the problem in his circuit, discover its cause, and often indicate what should be changed to achieve the desired performance. It is perhaps an irony that the most advanced digital equipment is still being analysed for both software and hardware 'glitches' by using oscilloscopes, when and where ordinary logic analysers fail or just offer lower resolution. Originally the most important element of an oscilloscope was its display, the cathode ray tube (CRT), which whilst offering the possibility of direct signal observation also presented the most challenging problems for the amplifiers driving it. An oscilloscope. Today the CRT has been replaced by LCD screens in almost all oscilloscopes, and inevitably most of its internal circuitry has been replaced by powerful microprocessors, with the exception of the signal input stage: the signal still needs to be taken from its source or another analog circuit in such a way that the source will not be overloaded, and then needs to be amplified and manipulated to a suitable level by analog circuitry before finally being converted into a digital form. The replacement of further heavy amplification by cheap digital circuity of course contributes to the reduction of prices, with the consequence that even the poorest of labs can now afford an oscilloscope, leading to a wide proliferation of the instrument.
CRT screen. So now, instead of highly trained specialists or graduate engineers, most of the lab personnel can be general technicians, who eventually need to understand what they are looking at on the screen, and act accordingly. Thus the potential market for our book is increasing steadily. Of course, very few of those technicians will become oscilloscope designers themselves. Nevertheless, being able to understand the inner working of high speed amplifier circuits, where not only its active and passive components, but also the geometry of the layout plays an important role, allows one to apply those same physical principles and technical experience to other, maybe even unrelated problems, and arrive at a solution more quickly. At this occasion I would like to expose a peculiar problem of the time domain system response calculation, which seems to be not widely known among engineers, and even if known, it is often considered too difficult and thus almost never used. It is the problem of the so called convolution integral. If you belong to the vast majority of people, who during their education have been inoculated to feel a certain uneasiness at the mentioning of mathematics (if not open hatred), please do not be intimidated, I am not going to bother you with all the details. It is true that convolution integral presents a demanding task even to a skilled mathematician, and in many cases the functions being treated may even not have an analytical solution at all (meaning that it is impossible to solve it using ordinary mathematical tools). But it is also true that numerical solutions almost always exist! In fact, as a matter of principle, all (natural and artificial) energy processes can be described by a convolution integral of two or more simple functions. Indeed, during our education we have been conditioned to regard natural phenomena as functions of time: things change as time passes. And to be able to see those changes we often construct a plot showing a point for point relation between instants in time and the states of the observed phenomenon. This is often possible owed to some very clever simplification of the laws of nature which any real system has to follow. However, all changes are changes of local energy states, and energy processes are not functions of instantaneous time; rather, they are functions of all the history experienced by the system in question, though weighted by its own relaxation function. This may sound complicated, but what I want to show is that by exploiting the power of modern computers it is very easy to calculate such processes exactly (approximated only by the choices of resolution and the basic time step, since we want to complete the task in some finite time and with finite capabilities of the machine at our disposal, but it is always possible to trade off the calculation time for accuracy). So, being functions of history, such problems are ideally tackled by convolution integrals. As an example, think of a system having its own relaxation function, and being forced by some external function into a new state of equilibrium. The system may be a pendulum, which after being pulled away from the vertical will regain its equilibrium after a number of oscillations (depending on the system damping: a pendulum immersed in an oil bath will need maybe only a single oscillation). Or it may be a spring with a weight, or in electrical terms, it may be a network built of inductance, capacitance, and resistance elements. It really does not matter, since we can describe the system by the same physical and mathematical model equations. The important question is: if we know the system's own relaxation function and the external forcing function, how will the system react to the external forcing, how will it transition from a previous equilibrium state to the new state imposed by the external forcing function?
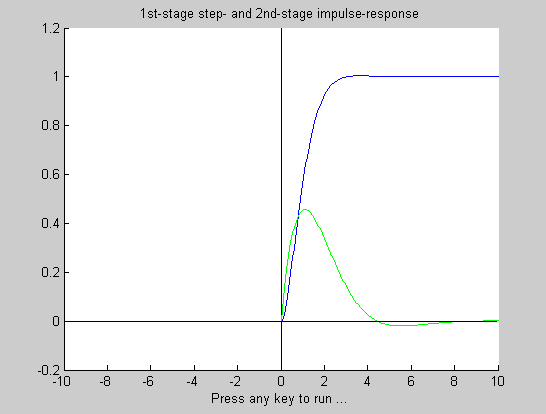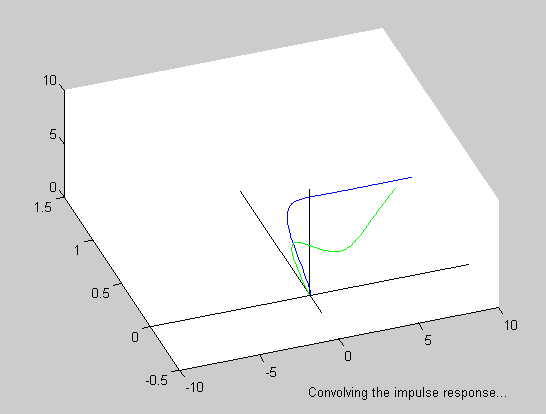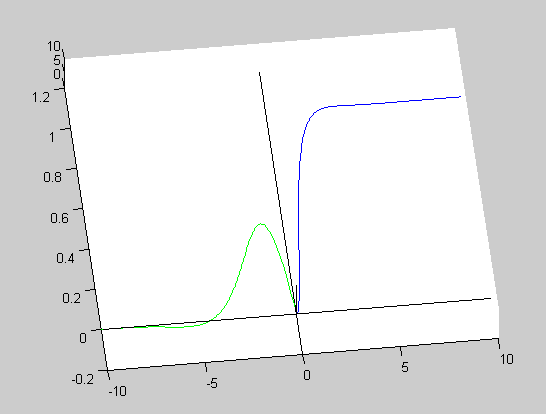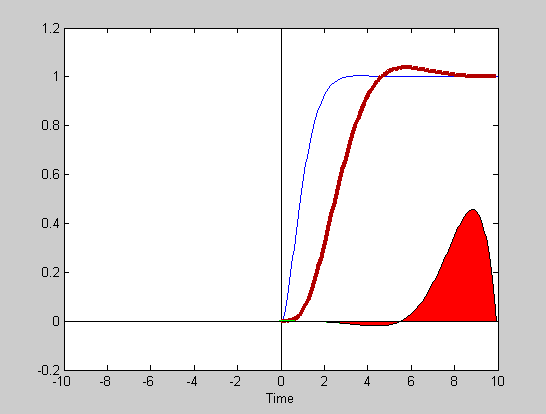
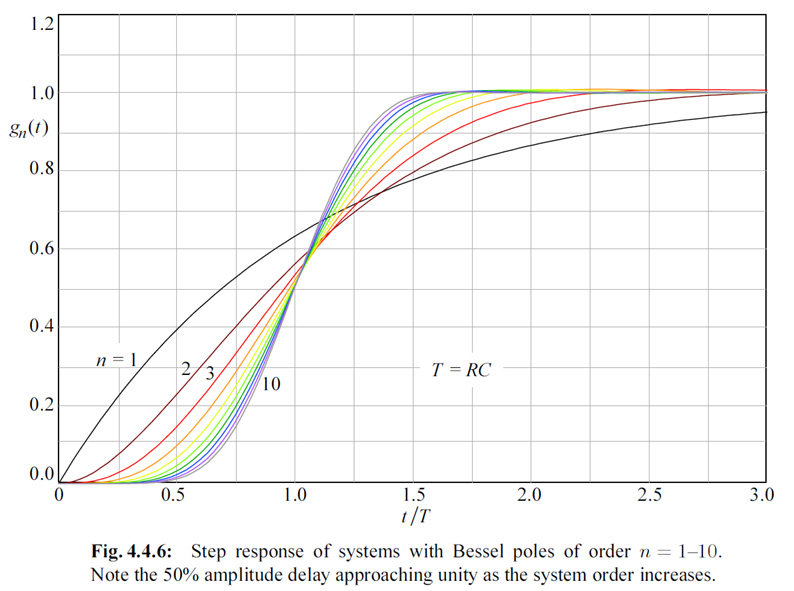
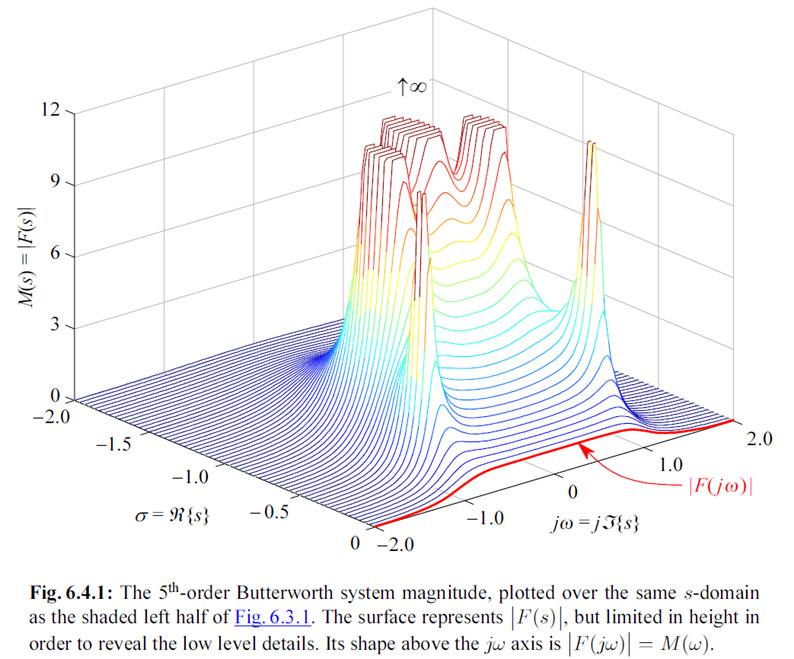
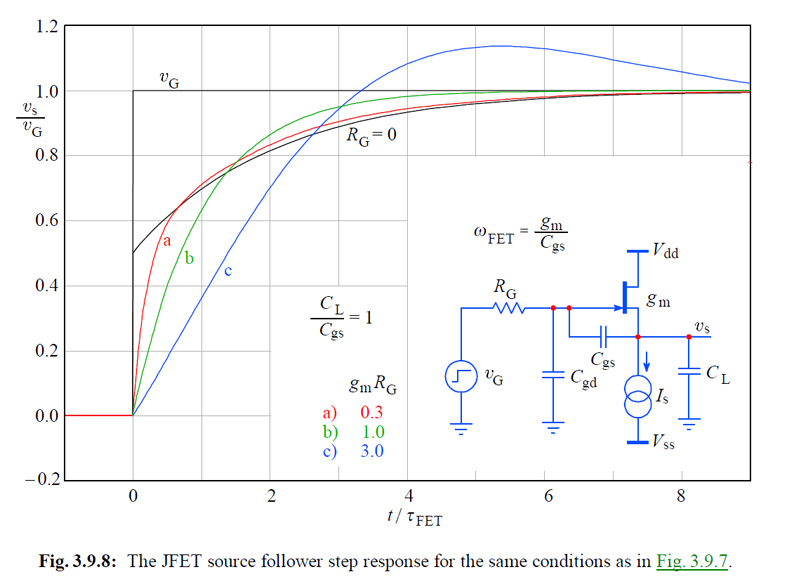
The GIFF animation alongside shows the answer for such an example. First the system's relaxation function (also known as the impulse response) must be convolved, or time-folded about the chosen initial time point. Then this folded function is sliding along the time axis, partially and eventually completely overlaying with the forcing function. At each time point we multiply the two overlaying parts and integrate (sum) all the overlaying time points. Each integration is equal to the area under the resulting multiplication, representing the instantaneous value of the system's response. Thus every response time point depends not on the instantaneous value of the forcing function, but on all the previous time points of the multiplied forcing and impulse functions. This is a very important consideration of how nature works, not just from the engineering point of view, but also from the physical and philosophical point of view. In our book we present detailed mathematical derivation of various system functions in analytic form, and we give detailed development of computer algorithms for a complete characterization of the system response both in the frequency and time domain. Time domain response optimization is given special attention. And the approach to problems is from the design engineer's perspective, intended to provide the optimal performance reference to which the actual realization can be compared, and eventually improved. Since the physical principles presented are universal and essentially technology independent, they can be applied at any level of complexity and any stage of realization, from the compensation of chip's bonding parasitic inductance, to the optimization of a complete system, even of such systems which are partially realized in hardware and partially in software. We are confident that with such approach the book can serve as a good learning companion for young engineering students, as well as a reference for experienced engineers. The following are some examples of the graphical material from the book.
Formatted for CROWN by Marko Puljic |